UTS Routing (Detailed)

The inputs and outputs of the algorithm for University Transit Service (UTS) Routing are straightforward. Given the latitude and longitude of a user's location and the latitude and longitude of their destination as inputs, output the series of bus rides and/or walking that results in reaching the destination the fastest. I do this by representing the problem as a graph. The user's location, the destination, and every bus stop is one node in the graph. Each directed edge in the graph represents either walking or a bus traveling between two stops. I then run Dijkstra's algorithm on this graph to find the shortest path between the user's location and the destination. The implementation itself can logically be divided into three parts, each of which is described below: Creating The Graph, Using Dijkstra's algorithm, and Displaying the Results.

Creating the Graph

The first part of the algorithm is probably the most challenging. The goal is to parse through all of the bus stop, route, and arrival estimate information to create a graph that Dijkstra's algorithm can be run on. This requires several APIs. I use the TransLoc PublicAPI to get the list of all bus stops, all routes, and all arrival estimates.


    # URLs for the TransLoc API
    stops_url = "https://transloc-api-1-2.p.rapidapi.com/stops.json"
    routes_url = "https://transloc-api-1-2.p.rapidapi.com/routes.json"
    arrival_estimates_url = "https://transloc-api-1-2.p.rapidapi.com/arrival-estimates.json"

    host = "transloc-api-1-2.p.rapidapi.com"
    agencies = "347" # UVA

    with open("TransLocKey.txt", "r") as fp:
      transloc_key = fp.readline()

    headers = {"x-rapidapi-host": host, "x-rapidapi-key": transloc_key}
    payload = {"agencies": agencies}

    stops_response = requests.get(stops_url, headers=headers, params=payload)
    stops_json = stops_response.json()

    routes_response = requests.get(routes_url, headers=headers, params=payload)
    routes_json = routes_response.json()

    arrival_estimates_response = requests.get(arrival_estimates_url, headers=headers, params=payload)
    arrival_estimates_json = arrival_estimates_response.json()

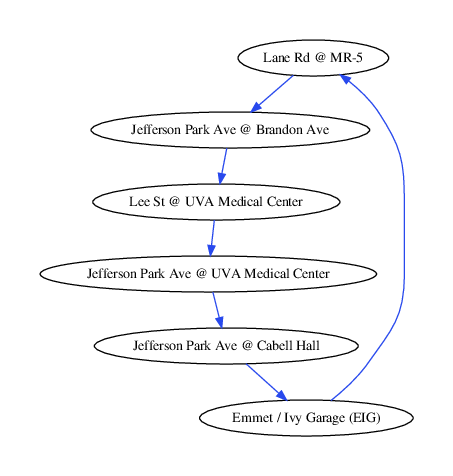
There are a couple problems with this. First, TransLoc gives me a list of every single bus stop and every single route, including those that are not being serviced at the time of the request. In order to filter all of these out, I add nodes to the graph only if they have arrival estimates. Second, TransLoc does not provide the ordering of the bus stops along a route. Again, I solve this problem using the arrival estimates information. For each route, I order the stops by the arrival estimates of one of the buses on that route. Then, I add directed edges to the graph that connect the stops in order. Here is an example of a single route (the Blueline in UVA's UTS).

At this point, the graph contains one node for every bus stop and has all stops connected by their route. Next, I add two more stops: one for the user's location and one for the destination. I also add edges from the user's location to every other node and from node to the destination. These edges are for walking. I use Google's Distance Matrix API to find estimated walking times for all of these edges. Note that I do not add edges between the bus stops for walking and, thus, this algorithm will never require a user to walk between bus stops. I do this purposefully because I view it as a tradeoff. In order to allow for this, I would need to add edges between every pair of stops, making the graph fully connected. I believe that the fastest path will require walking between bus stops rarely enough that it's worth it for the algorithm to avoid the complexity of a fully connected graph. Occasionally the algorithm will return a suboptimal path in exchange for every run of the algorithm being faster and less complex.

Google's Distance Matrix API also has an issue where it doesn't always preserve the triangle inequality. Sometimes Google says that it's faster to walk from A to B to C than it is to walk directly from A to C. I check for this and correct it after Dijkstra's algorithm has found the shortest path. At this point, we now have a graph that we can run Dijkstra's algorithm on. Here is the entire graph generated for UVA's UTS in the early afternoon.

Using Dijkstra's algorithm

Once the graph has been created, we can use Dijkstra's algorithm to find the shortest path. If you're not familiar with the single-source shortest path problem or with Dijkstra's algorithm, Wikipedia has a great page on it. What makes this application of Dijkstra's algorithm interesting is that the graph's edge weights change over time. Choosing to walk to a bus stop that is 10 minutes away instead of one that is 15 minutes away will put all of the buses in different positions. In general, a graph with changing edge weights requires a dynamic version of Dijkstra's algorithm, like the one that I've implemented here. However, we can make a couple of interesting observations about the nature of this graph's changes to avoid most of that commplexity.

One of the reasons that Dijkstra's algorithm works is that, when a node is extracted from the priority queue, we are guaranteed to have already found the shortest path to that node. Once a node is extracted, the path to that node is fixed. The violation of this property is what requires some of the more interesting data structures in the dynamic version of the algorithm. However, this property is not violated by the context of this problem. Once we've extracted a node from the priority queue, we have to consider what implications selecting that node had on the rest of the graph. The buses will all have moved by the time we reached that node, meaning that we have to consider a version of the graph that has been properly updated with all of these movements. However, the graph is never updated in a way that would allow us to have reached a previously extracted node in a faster way. We never find a faster path to a node that we've already found the fastest path to. For this reason, we can use a pretty straightforward version of Dijkstra's algorithm.

One other consideration that we need to keep in mind is that we may have to wait at a bus stop. It may only take a bus 5 minutes to travel from Stop A to Stop B, but if the next bus won't arrive at Stop A for 35 minutes, there's probably a faster way. I handle the graph's dynamic nature as well as this waiting issue by not using traditional edge weights. Instead, I keep track of what the time at which I can be at any given stop. Then, during the relaxation part of Dijkstra's algorithm, I check to see if the edge that I'm considering will allow me to get to the next stop at an earlier time than the time saved at that stop. If the time is 10:03 and walking to a stop will take twenty minutes, I give that stop a time of 10:23. If I then find a way to use a bus to get there in ten minutes, the stop is updated to have a time of 10:13.

So far, this is not really much different than a traditional implementation of Dijkstra's algorithm. The difference is that when I'm considering an edge in the relaxation step, I don't compare the sum of the current node's time and the edge weight to the next node's time. In other words, I don't do the u.d + w(u,v) < v.d comparison. Instead, I take the time at my current node and find the next time that a bus will arrival at the next node. I compare this arrival time with the next node's time and, if it's sooner, then I know it will be faster to take the bus to the next node. This way, if I'm "on the bus" at my current node, the arrival estimate at my next node will be equal to the time it takes the bus to drive there. If, however, I have to wait at the current node for a bus, the waiting time will be taken into account when I look at the arrival time of a bus at the next node. This method also has a couple of other benefits. Some bus stops are on multiple routes, and this method provides an easy way of considering whether it's faster to stay on my current bus or to get off at the stop and wait for a different bus coming via a different route. It's also common for bus drivers to spend a long time at one stop to take a break, switch drivers, or get back on schedule if the bus is running early. If a bus is spending a long time at one stop, this will be reflected in its arrival estimates, and thus this method will take it into account. Here's an abbreviated version of my implementation of Dijkstra's algorithm:


    while g.nodes[DST_ID] in pq:
      u = pq.pop_task()
      u.unvisited = False

      for e in g.adj_list[u.stop_id]:
        v = g.nodes[e.to_stop]

        if v.unvisited:
          # Find the next time a bus on e's route is arriving at u
          arrivals = [ar for ar in u.arrival_times[e.route_id] if ar >= u.time]

          # If we don't have an arrival estimate for any buses on this route
          # at the current stop, then we assume that we'd have to wait a
          # long time for the next bus (longer than what the TransLoc API
          # returns by default), and thus we don't consider this edge
          if len(arrivals) > 0:
            next_arrival = min(arrivals)
          else:
            continue

          # Find the vehicle ID of the bus arriving at that time
          next_bus = u.buses[next_arrival]

          # Find the first time that the same bus arrives at the next stop
          # after it already arrived at this stop. This is the time at which
          # we would arrive at v if we traveled along edge e
          arrivals_at_v = [ar for ar in v.arrival_times[e.route_id] if v.buses[ar] == next_bus and ar > next_arrival]
          arrival_at_v = min(arrivals_at_v)

          if arrival_at_v < v.time:
            v.time = arrival_at_v
            v.p = e
            pq.update_task(v, v.time)

Displaying the Results

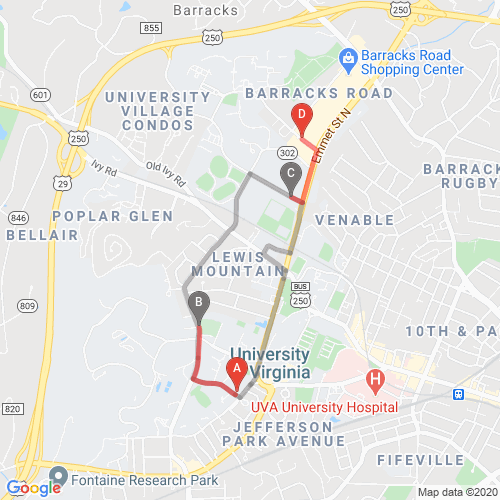
I use Google's Static Maps API for displaying the fastest path because it allows for the inclusion of custom markers and paths on the map. I display a marker at the user's location, the destination, and every bus stop on the path to the destination. Unfortunately, while TransLoc provides encoded polylines to display the bus routes on the map, it doesn't provide a separate encoded polyline for each segment between stops. So, instead of only displaying the relevant portion of the bus route, I need to either display all or none of it. Below is an image showing the fastest way to get from Rice Hall to John Paul Jones Arena at UVA (a route I've taken many times).